双原子分子的热容曲线/小课题

Posted on 2022-01-13 In 报告 Views: Symbols count in article: 3.9k Reading time ≈ 4 mins.

1 前言

本文是笔者在《化学中的数学》课的期末课题研究内容。对于没有学过物理化学的我来说，一开始觉得不易理解，但当为了这课题去查阅资料，立刻就发现了小练习：转动热容 - 知乎 (zhihu.com).接下来看了统计物理的书，又发现解决问题需要的公式全都写在书上了，只需照着公式写程序就好。但讲报告的ddl在即，没有换题目的时间了，便只能在这上面想办法做得丰富些。

关于这个的想法最早是学普物热学的时候，看到氢气的热容曲线，就在想自由度依次激发这件事由理论应当如何描述。期末课题的内容（第二题）是对任意分子体系建立模型，得到一些热力学、动力学量，我想起了它。同学们有的在尝试PIMD，有的在给分子建立神奇力场模型，还有学长在做分子动力学模拟的程序，我看着自己的热容曲线，觉得做了件挺无聊的事。

不过还是记下来了。刚好有写好的报告，改一改就能发出来了。

2 理论模型

2.1 理想玻尔兹曼气体

说起来我半天没想明白“激发”是怎么一回事，或者说热容上升的那段背后的数学是什么样的。后来想了想，有没有可能把配分函数之类的写出来，它的数学形式就自然蕴含了“逐渐激发”的行为。查了书以后好像的确是这么一回事，这些量子行为看起来就是级数和的性质所决定，而与积分的结果相区别。

我们从气体的正常沸点开始考虑。由于满足非简并条件，可忽略费米子/玻色子的差异，气体遵从玻尔兹曼统计。分子的能量可分为独立的平动、转动、振动和电子能项，如此得配分函数为： \[ Z = Z_{\text{trans}}Z_{\text{rot}}Z_{\text{vib}}Z_e \] 而自由能、能量均值与配分函数的关系是 \[ F = \ln Z \quad \braket{H} = -\frac{\partial \ln Z}{\partial \beta} \]

故等容热容，依据定义为 \[ c_V = \frac{\partial}{\partial T}\langle{H}\rangle = c_{\text{trans}}+c_{\text{rot}}+c_{\text{vib}} \]

考虑的温度范围应离气体的解离温度较远，这时可认为电子都处于基态，$Z_e=1$，从而对热容无贡献。 (1)式说明可分别处理各部分热容。

2.2 平动热容

跟据一维无穷深势阱的结果，平动配分函数为 \[ Z_t = \frac{V}{h^3}\left( \frac{2\pi m}{\beta}\right)^{\frac{3}{2}} \tag{2} \] 这一结论的得出假设了能级差很小，从而可以把求和变为积分处理。 \[ \Delta\varepsilon \sim \frac{2\pi^2 \hbar^2}{m L} \] 能级差远远小于$k_BT$的量级，这在我们的研究范围内是总能满足的。

所以认为(2)总是成立的，从而有 \[ c_{\text{trans}} = \frac{3}{2}Nk_BT \]

2.3 转动热容

转动能级来自于角动量本征问题的求解，其结果为： \[ \varepsilon_n = \frac{\hbar^2}{2I}K(K+1) \qquad K=0,1,2\dots \]

而有$2K+1$的简并度。得到配分函数为： \[ Z_r = \sum_{K=0}^\infty(2K+1)\exp(-K(K+1)\frac{\hbar^2\beta}{2I})\tag{3} \]

其中，$\theta_r = {\hbar^2}\big/{2Ik_B}$ 称为转动特征温度，可在书中查到。此式需要数值计算，由于这一级数的收敛性依赖于$e$指数，故不能逐项简化。因此不考虑 $c_{\text{rot}}$ 的解析形式。

(3)式对于异核双原子分子是适用的，对于同核分子如H$_2$、D$_2$，核是玻色子或费米子，对分子波函数的对称性有要求。

氢核是费米子，要求分子的$\Psi$反对称，由于$\Psi = \Psi_{\text{spin}}\Psi_{\text{rot}}$，核自旋态对转动本征态有限制：自旋平行，$K$只能取偶数；自旋相反，$K$只能取奇数。即区分为正氢、仲氢，其比例是3/1。

以下是修正后的氢分子配分函数。 \[ \begin{cases} Z_{r} = \frac{3}{4}Z_{r}^{\text{odd}}+\frac{1}{4}Z_{r}^{\text{even}} \\ Z_{r}^{\text{odd}} = \sum_{K = 1,3,5\dots}z(K) \\ Z_{r}^{\text{even}} = \sum_{K = 0,2,4\dots}z(K) \end{cases} \tag{4} \]

2.4 振动热容

常见的结果来自谐振子模型，由 \[ Z_{v} = \frac{1}{2\sinh(\beta\hbar\omega/2)} \]

得到热容的解析表达式： \[ c_{\text{vib}} = (\beta\hbar\omega)^2\frac{e^{\beta\hbar\omega}}{(e^{\beta\hbar\omega} - 1)^2}Nk_B \]

3 计算部分

3.1 H$_2$转动配分函数、热容的处理

在计算中为了方便，取$k_B = 1$，或者结果以$Nk_B$的倍数表示。

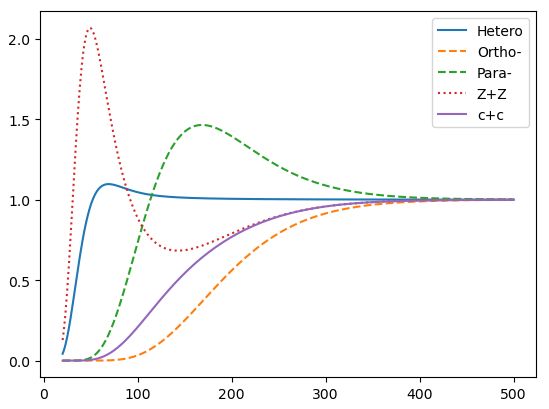
H$_2$的转动热容

(3)级数的收敛性很好，$K$取100就保证收敛。

使用差分方法，求出转动能量均值，再求出热容。这里取差分的间隔为 0.00001, 过小的间隔会带来不稳定的结果。

按图例所示顺序，第一条(Hetero)为异核双原子分子的转动热容，可见经过一个极大值后迅速趋于经典极限结果。(Ortho-)和(Para-)分别表示了正氢、仲氢的计算结果，它们的性质有较大的差异。利用修正的配分函数(4)计算出的曲线如点线(Z+Z)所示，和实验得到的结果完全不同。而(c+c)曲线是用正氢、仲氢热容按照其所占比例加权平均的结果，与实验符合。

这是因为，实际的核自旋很难在碰撞中发生改变，其行为相当于是独立的。所以氢气体系是正氢、仲氢的非平衡混合态，自由能是直接相加的关系。

3.2 各种分子的热容曲线

在谐振子近似下，代入分子的转动、振动特征温度信息(D$_2$加上正、仲之比），整体的热容曲线容易得出，如下图（20--50000K)：

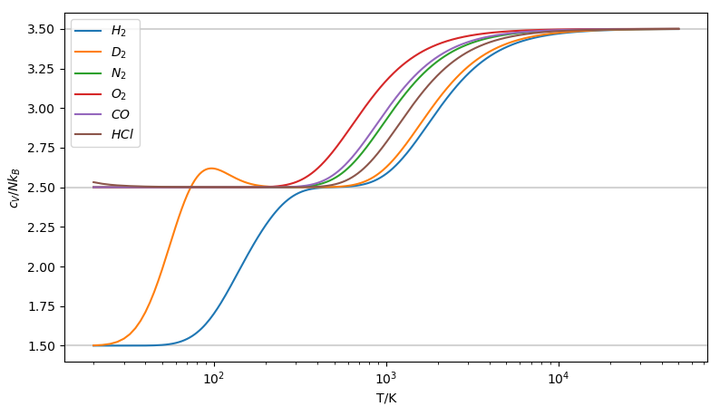
等体热容曲线

可以看到从20 K开始，除了H和D，其他分子的转动热容是一直激发的，在研究范围内都趋于$1Nk_B$的经典结果，这是一个有效的近似。也因此人们一般只对H和D有正、仲之分。

在计算过程中发现热容曲线在右端有的上升、有的下降，偏离了经典极限的结果。经排查是转动热容的结果在高温时发生了变化，这应该是差分计算时的问题，和高温极限的结果不同。所以手动调节为1，修正后得到符合实验结果的图2。

同样的方法对更多分子有效，只需知道特征温度。在转动动热容都已激发的条件下，此模型下不同分子的曲线相当于平移。

在200--300 K范围，振动热容基本都未激发，但随温度升高逐步开始激发。在$10^2\sim 10^4$的研究范围内，振动热容是不符合"高温极限"的，因此需要特殊考虑。

3.3 N$_2$的Morse振子模型

引入Morse势更精确描述分子的振动。这里以N$_2$为例 \[ V(r) = D_e\left(1-e^{-a(r-r_e)}\right)^2 \]

其中，$ D_e $查到为79845 $ ^{-1} $ ，换算为 0.36380 hatree 或 114879 K（即解离温度）。

$ = a $，延用之前的$ $得到$ a $。与谐振子势的对比如下图

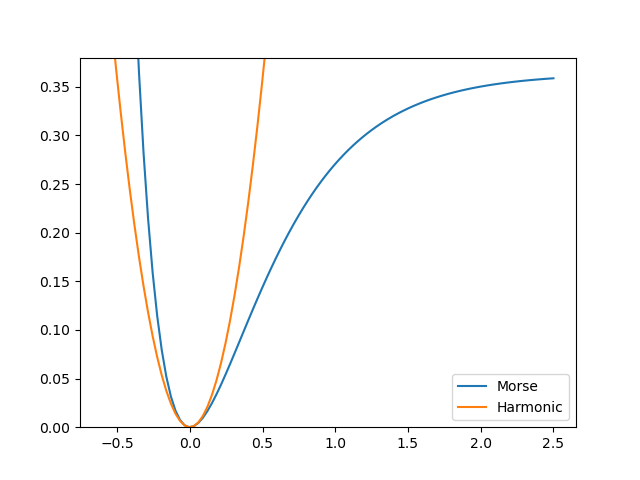
Morse / H.O. Potential

Morse振子的本征能级为 \[ E_n = \hbar\omega\left(n+\frac{1}{2}\right) - \frac{\left[\hbar\omega\left(n+\frac{1}{2}\right)\right]^2}{4D_e} \] 据此计算配分函数，然后数值计算得到振动热容。与谐振子势的结果对比如下：

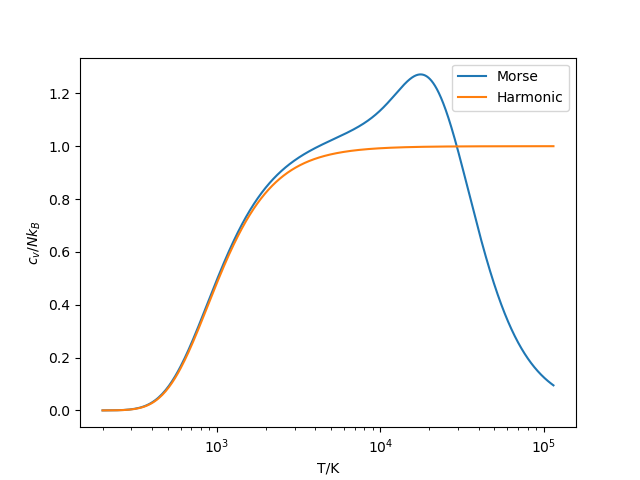
振动热容对比

可见Morse势的结果在高温下并不趋于常数，而是上升至一个极大值，在接近解离温度时热容逐渐下降。由于时间紧张，并未对结果进行验证。而其上升和下降的行为应当是比较符合实际的。在较低温度的部分两条曲线基本重合，这是简谐近似有效的部分。到$10^4$附近两条曲线的差异就很明显，所以考虑非谐振效应是很有必要的。

3.4 基于涨落的热容曲线

本来还想尝试助教提供的采样方法，利用 \[ \int \mathrm{d}\Gamma \, e^{-\beta H/Q} H^2 = \left(e^{-\beta_0 H/Q}\right)\int \mathrm{d}{\Gamma}\, e^{-(\beta-\beta_0)H/Q}H^2 \]

从哈密顿量的涨落出发计算热容。与上述用了很多结论的方法应能得出一样的效果。但由于时间有限，无法进行这一部分了。

4 总结

主要是得到了一些"经典极限"之外的结果，并以此检验了各种近似的正确性，结果是通用的。转动热容部分，对于较复杂的H$_2$、D$_2$做了特殊处理和分析。振动热容部分考虑了谐振子和Morse振子两种模型的差异。

由于之前并未学过物理化学，补理论知识花费了不少时间。在研究的过程中感觉对一些热力学和统计物理的知识，以及对几种模型了解更深了些。也算是一定程度上达成了目的。

参考文献

[1] 热力学与统计物理学, 林宗涵

[2] Statistical Physics (5th Edition), L. D. Landau

[3] https://en.wikipedia.org/wiki/Morse_potential

[4] 物理化学讲义, 彭笑刚

[5] Le Roy, Huang, and Jary, J. Chem. Phys., 125, 164310 (2006)